Chapter 10, K-Nearest-Neighbors example
In this chapter we will explore several data visualizations of the K-Nearest-Neighbors (KNN) classifier.
Chapter outline:
- We will start with the original static data visualization, re-designed as two ggplots rendered by animint. There is a plot of 10-fold cross-validation error, and a plot of the predictions of the 7-Nearest-Neighbors classifier.
- We propose a re-design that allows selecting the number of neighbors used for the model predictions.
- We propose a second re-design that allows selecting the number of folds used to compute the cross-validation error.
Original static figure
We start by reproducing a static version of Figure 13.4 from Elements of Statistical Learning by Hastie et al. That Figure consists of two plots:
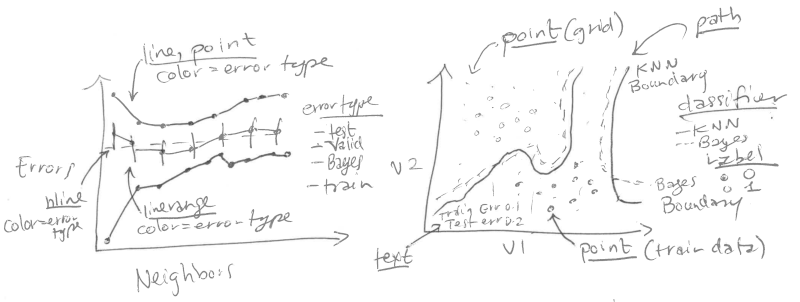
Left: mis-classification error curves, as a function of the number of neighbors.
geom_lineandgeom_pointfor the error curves.geom_linerangefor error bars of the validation error curve.geom_hlinefor the Bayes error.- x = neighbors.
- y = percent error.
- color = error type.
Right: data and decision boundaries in the two-dimensional input feature space.
geom_pointfor the data points.geom_pointfor the classification predictions on the grid in the background.geom_pathfor the decision boundaries.geom_textfor the train/test/Bayes error rates.
Plot of mis-classification error curves
We begin by loading the data set.
if(!file.exists("ESL.mixture.rda")){
download.file(
"https://web.stanford.edu/~hastie/ElemStatLearn/datasets/ESL.mixture.rda",
"ESL.mixture.rda")
}
load("ESL.mixture.rda")
str(ESL.mixture)## List of 8
## $ x : num [1:200, 1:2] 2.5261 0.367 0.7682 0.6934 -0.0198 ...
## $ y : num [1:200] 0 0 0 0 0 0 0 0 0 0 ...
## $ xnew : 'matrix' num [1:6831, 1:2] -2.6 -2.5 -2.4 -2.3 -2.2 -2.1 -2 -1.9 -1.8 -1.7 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:6831] "1" "2" "3" "4" ...
## .. ..$ : chr [1:2] "x1" "x2"
## $ prob : num [1:6831] 3.55e-05 3.05e-05 2.63e-05 2.27e-05 1.96e-05 ...
## ..- attr(*, ".Names")= chr [1:6831] "1" "2" "3" "4" ...
## $ marginal: num [1:6831] 6.65e-15 2.31e-14 7.62e-14 2.39e-13 7.15e-13 ...
## ..- attr(*, ".Names")= chr [1:6831] "1" "2" "3" "4" ...
## $ px1 : num [1:69] -2.6 -2.5 -2.4 -2.3 -2.2 -2.1 -2 -1.9 -1.8 -1.7 ...
## $ px2 : num [1:99] -2 -1.95 -1.9 -1.85 -1.8 -1.75 -1.7 -1.65 -1.6 -1.55 ...
## $ means : num [1:20, 1:2] -0.2534 0.2667 2.0965 -0.0613 2.7035 ...We will use the following components of this data set:
x, the input matrix of the training data set (200 observations x 2 numeric features).y, the output vector of the training data set (200 class labels, either 0 or 1).xnew, the grid of points in the input space where we will show the classifier predictions (6831 grid points x 2 numeric features).prob, the true probability of class 1 at each of the grid points (6831 numeric values between 0 and 1).px1, the grid of points for the first input feature (69 numeric values between -2.6 and 4.2). These will be used to compute the Bayes decision boundary using the contourLines function.px2, the grid of points for the second input feature (99 numeric values between -2 and 2.9).means, the 20 centers of the normal distributions in the simulation model (20 centers x 2 input features).
First, we create a test set, following the example code from help(ESL.mixture). Note that we use a data.table rather than a data.frame to store these big data, since data.table is often faster and more memory efficient for big data sets.
library(MASS)
library(data.table)
set.seed(123)
centers <- c(
sample(1:10, 5000, replace=TRUE),
sample(11:20, 5000, replace=TRUE))
mix.test <- mvrnorm(10000, c(0,0), 0.2*diag(2))
test.points <- data.table(
mix.test + ESL.mixture$means[centers,],
label=factor(c(rep(0, 5000), rep(1, 5000))))
test.points## V1 V2 label
## <num> <num> <fctr>
## 1: 2.0210959 1.390512445 0
## 2: 2.7488414 1.032724096 0
## 3: 2.2631823 0.003595182 0
## 4: 0.9215398 0.880968101 0
## 5: 1.8492359 -0.807985255 0
## ---
## 9996: -2.0939980 1.602554853 1
## 9997: 1.6409142 0.889177271 1
## 9998: 0.9861499 0.936203846 1
## 9999: -1.9089417 1.613524647 1
## 10000: 0.7678115 0.315426519 1We then create a data table which includes all test points and grid points, which we will use in the test argument to the knn function.
pred.grid <- data.table(ESL.mixture$xnew, label=NA)
input.cols <- c("V1", "V2")
names(pred.grid)[1:2] <- input.cols
test.and.grid <- rbind(
data.table(test.points, set="test"),
data.table(pred.grid, set="grid"))
test.and.grid$fold <- NA
test.and.grid## V1 V2 label set fold
## <num> <num> <fctr> <char> <lgcl>
## 1: 2.0210959 1.390512445 0 test NA
## 2: 2.7488414 1.032724096 0 test NA
## 3: 2.2631823 0.003595182 0 test NA
## 4: 0.9215398 0.880968101 0 test NA
## 5: 1.8492359 -0.807985255 0 test NA
## ---
## 16827: 3.8000000 2.900000000 <NA> grid NA
## 16828: 3.9000000 2.900000000 <NA> grid NA
## 16829: 4.0000000 2.900000000 <NA> grid NA
## 16830: 4.1000000 2.900000000 <NA> grid NA
## 16831: 4.2000000 2.900000000 <NA> grid NAWe randomly assign each observation of the training data set to one of ten folds.
n.folds <- 10
set.seed(2)
mixture <- with(ESL.mixture, data.table(x, label=factor(y)))
mixture$fold <- sample(rep(1:n.folds, l=nrow(mixture)))
mixture## V1 V2 label fold
## <num> <num> <fctr> <int>
## 1: 2.526092968 0.3210504 0 5
## 2: 0.366954472 0.0314621 0 8
## 3: 0.768219076 0.7174862 0 6
## 4: 0.693435680 0.7771940 0 10
## 5: -0.019836616 0.8672537 0 6
## ---
## 196: 0.256750222 2.2936046 1 1
## 197: 1.925173384 0.1650526 1 3
## 198: 1.301941035 0.9921996 1 6
## 199: 0.008130556 2.2422639 1 4
## 200: -0.196246334 0.5514036 1 8We define the following OneFold function, which divides the 200 observations into one train and one validation set. It then computes the predicted probability of the K-Nearest-Neighbors classifier for each of the data points in all sets (train, validation, test, and grid).
OneFold <- function(validation.fold){
set <- ifelse(mixture$fold == validation.fold, "validation", "train")
fold.data <- rbind(test.and.grid, data.table(mixture, set))
fold.data$data.i <- 1:nrow(fold.data)
only.train <- subset(fold.data, set == "train")
data.by.neighbors <- list()
for(neighbors in seq(1, 30, by=2)){
if(interactive())cat(sprintf(
"n.folds=%4d validation.fold=%d neighbors=%d\n",
n.folds, validation.fold, neighbors))
set.seed(1)
pred.label <- class::knn( # random tie-breaking.
only.train[, input.cols, with=FALSE],
fold.data[, input.cols, with=FALSE],
only.train$label,
k=neighbors,
prob=TRUE)
prob.winning.class <- attr(pred.label, "prob")
fold.data$probability <- ifelse(
pred.label=="1", prob.winning.class, 1-prob.winning.class)
fold.data[, pred.label := ifelse(0.5 < probability, "1", "0")]
fold.data[, is.error := label != pred.label]
fold.data[, prediction := ifelse(is.error, "error", "correct")]
data.by.neighbors[[paste(neighbors)]] <-
data.table(neighbors, fold.data)
}#for(neighbors
do.call(rbind, data.by.neighbors)
}#for(validation.foldBelow, we run the OneFold function in parallel using the future package. Note that validation folds 1:10 will be used to compute the validation set error. The validation fold 0 treats all 200 observations as a train set, and will be used for visualizing the learned decision boundaries of the K-Nearest-Neighbors classifier.
future::plan("multisession")
data.all.folds.list <- future.apply::future_lapply(
0:n.folds, function(validation.fold){
one.fold <- OneFold(validation.fold)
data.table(validation.fold, one.fold)
},
future.seed = NULL)
(data.all.folds <- do.call(rbind, data.all.folds.list))## validation.fold neighbors V1 V2 label set
## <int> <num> <num> <num> <fctr> <char>
## 1: 0 1 2.021095933 1.390512445 0 test
## 2: 0 1 2.748841354 1.032724096 0 test
## 3: 0 1 2.263182259 0.003595182 0 test
## 4: 0 1 0.921539757 0.880968101 0 test
## 5: 0 1 1.849235932 -0.807985255 0 test
## ---
## 2810111: 10 29 0.256750222 2.293604575 1 train
## 2810112: 10 29 1.925173384 0.165052639 1 train
## 2810113: 10 29 1.301941035 0.992199616 1 train
## 2810114: 10 29 0.008130556 2.242263910 1 train
## 2810115: 10 29 -0.196246334 0.551403559 1 train
## fold data.i probability pred.label is.error prediction
## <int> <int> <num> <char> <lgcl> <char>
## 1: NA 1 0.0000000 0 FALSE correct
## 2: NA 2 0.0000000 0 FALSE correct
## 3: NA 3 0.0000000 0 FALSE correct
## 4: NA 4 0.0000000 0 FALSE correct
## 5: NA 5 0.0000000 0 FALSE correct
## ---
## 2810111: 1 17027 0.8275862 1 FALSE correct
## 2810112: 3 17028 0.5517241 1 FALSE correct
## 2810113: 6 17029 0.7931034 1 FALSE correct
## 2810114: 4 17030 0.7586207 1 FALSE correct
## 2810115: 8 17031 0.4137931 0 TRUE errorThe data table of predictions contains almost 3 million observations! When there are so many data, visualizing all of them at once is not practical or informative. Instead of visualizing them all at once, we will compute and plot summary statistics. In the code below we compute the mean and standard error of the mis-classification error for each model (over the 10 validation folds). This is an example of the summarize data table idiom which is generally useful for computing summary statistics for a single data table.
labeled.data <- data.all.folds[!is.na(label),]
error.stats <- labeled.data[, list(
error.prop=mean(is.error)
), by=.(set, validation.fold, neighbors)]
validation.error <- error.stats[set=="validation", list(
mean=mean(error.prop),
sd=sd(error.prop)/sqrt(.N)
), by=.(set, neighbors)]
validation.error## set neighbors mean sd
## <char> <num> <num> <num>
## 1: validation 1 0.240 0.01943651
## 2: validation 3 0.165 0.02362908
## 3: validation 5 0.165 0.02477678
## 4: validation 7 0.175 0.02713137
## 5: validation 9 0.195 0.03023060
## 6: validation 11 0.180 0.03000000
## 7: validation 13 0.170 0.02260777
## 8: validation 15 0.195 0.02629956
## 9: validation 17 0.205 0.02409472
## 10: validation 19 0.185 0.01833333
## 11: validation 21 0.180 0.01699673
## 12: validation 23 0.195 0.02166667
## 13: validation 25 0.190 0.01795055
## 14: validation 27 0.195 0.02034426
## 15: validation 29 0.205 0.02291288Below we construct data tables for the Bayes error (which we know is 0.21 for the mixture example data), and the train/test error.
Bayes.error <- data.table(
set="Bayes",
validation.fold=NA,
neighbors=NA,
error.prop=0.21)
Bayes.error## set validation.fold neighbors error.prop
## <char> <lgcl> <lgcl> <num>
## 1: Bayes NA NA 0.21other.error <- error.stats[validation.fold==0,]
head(other.error)## set validation.fold neighbors error.prop
## <char> <int> <num> <num>
## 1: test 0 1 0.2938
## 2: train 0 1 0.0000
## 3: test 0 3 0.2400
## 4: train 0 3 0.1300
## 5: test 0 5 0.2273
## 6: train 0 5 0.1300Below we construct a color palette from dput(RColorBrewer::brewer.pal(Inf, "Set1")), and linetype palettes.
set.colors <- c(
test="#377EB8", #blue
validation="#4DAF4A",#green
Bayes="#984EA3",#purple
train="#FF7F00")#orange
classifier.linetypes <- c(
Bayes="dashed",
KNN="solid")
set.linetypes <- set.colors
set.linetypes[] <- classifier.linetypes[["KNN"]]
set.linetypes["Bayes"] <- classifier.linetypes[["Bayes"]]
cbind(set.linetypes, set.colors)## set.linetypes set.colors
## test "solid" "#377EB8"
## validation "solid" "#4DAF4A"
## Bayes "dashed" "#984EA3"
## train "solid" "#FF7F00"The code below reproduces the plot of the error curves from the original Figure.
library(animint2)
errorPlotStatic <- ggplot()+
theme_bw()+
geom_hline(aes(
yintercept=error.prop, color=set, linetype=set),
data=Bayes.error)+
scale_color_manual(
"error type", values=set.colors, breaks=names(set.colors))+
scale_linetype_manual(
"error type", values=set.linetypes, breaks=names(set.linetypes))+
ylab("Misclassification Errors")+
xlab("Number of Neighbors")+
geom_linerange(aes(
neighbors, ymin=mean-sd, ymax=mean+sd,
color=set),
data=validation.error)+
geom_line(aes(
neighbors, mean, linetype=set, color=set),
data=validation.error)+
geom_line(aes(
neighbors, error.prop, group=set, linetype=set, color=set),
data=other.error)+
geom_point(aes(
neighbors, mean, color=set),
data=validation.error)+
geom_point(aes(
neighbors, error.prop, color=set),
data=other.error)
errorPlotStatic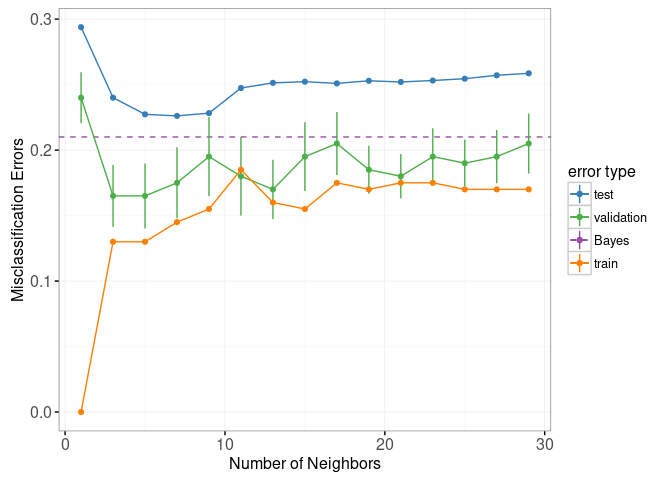
Plot of decision boundaries in the input feature space
For the static data visualization of the feature space, we show only the model with 7 neighbors.
show.neighbors <- 7
show.data <- data.all.folds[validation.fold==0 & neighbors==show.neighbors,]
show.points <- show.data[set=="train",]
show.points## validation.fold neighbors V1 V2 label set fold
## <int> <num> <num> <num> <fctr> <char> <int>
## 1: 0 7 2.526092968 0.3210504 0 train 5
## 2: 0 7 0.366954472 0.0314621 0 train 8
## 3: 0 7 0.768219076 0.7174862 0 train 6
## 4: 0 7 0.693435680 0.7771940 0 train 10
## 5: 0 7 -0.019836616 0.8672537 0 train 6
## ---
## 196: 0 7 0.256750222 2.2936046 1 train 1
## 197: 0 7 1.925173384 0.1650526 1 train 3
## 198: 0 7 1.301941035 0.9921996 1 train 6
## 199: 0 7 0.008130556 2.2422639 1 train 4
## 200: 0 7 -0.196246334 0.5514036 1 train 8
## data.i probability pred.label is.error prediction
## <int> <num> <char> <lgcl> <char>
## 1: 16832 0.1428571 0 FALSE correct
## 2: 16833 0.1428571 0 FALSE correct
## 3: 16834 0.2857143 0 FALSE correct
## 4: 16835 0.2857143 0 FALSE correct
## 5: 16836 0.2857143 0 FALSE correct
## ---
## 196: 17027 0.7142857 1 FALSE correct
## 197: 17028 0.8571429 1 FALSE correct
## 198: 17029 1.0000000 1 FALSE correct
## 199: 17030 0.8571429 1 FALSE correct
## 200: 17031 0.2857143 0 TRUE errorNext, we compute the Train, Test, and Bayes mis-classification error rates which we will show in the bottom left of the feature space plot.
text.height <- 0.25
text.V1.prop <- 0
text.V2.bottom <- -2
text.V1.error <- -2.6
error.text <- rbind(
Bayes.error,
other.error[neighbors==show.neighbors,])
error.text[, V2.top := text.V2.bottom + text.height * (1:.N)]
error.text[, V2.bottom := V2.top - text.height]
error.text## set validation.fold neighbors error.prop V2.top V2.bottom
## <char> <int> <num> <num> <num> <num>
## 1: Bayes NA NA 0.2100 -1.75 -2.00
## 2: test 0 7 0.2261 -1.50 -1.75
## 3: train 0 7 0.1450 -1.25 -1.50We define the following function which we will use to compute the decision boundaries.
getBoundaryDF <- function(prob.vec){
stopifnot(length(prob.vec) == 6831)
several.paths <- with(ESL.mixture, contourLines(
px1, px2,
matrix(prob.vec, length(px1), length(px2)),
levels=0.5))
contour.list <- list()
for(path.i in seq_along(several.paths)){
contour.list[[path.i]] <- with(several.paths[[path.i]], data.table(
path.i, V1=x, V2=y))
}
do.call(rbind, contour.list)
}We use this function to compute the decision boundaries for the learned 7-Nearest-Neighbors classifier, and for the optimal Bayes classifier.
boundary.grid <- show.data[set=="grid",]
boundary.grid[, label := pred.label]
pred.boundary <- getBoundaryDF(boundary.grid$probability)
pred.boundary$classifier <- "KNN"
Bayes.boundary <- getBoundaryDF(ESL.mixture$prob)
Bayes.boundary$classifier <- "Bayes"
Bayes.boundary## path.i V1 V2 classifier
## <int> <num> <num> <char>
## 1: 1 -2.600000 -0.528615 Bayes
## 2: 1 -2.557084 -0.500000 Bayes
## 3: 1 -2.500000 -0.459723 Bayes
## 4: 1 -2.484141 -0.450000 Bayes
## 5: 1 -2.407805 -0.400000 Bayes
## ---
## 246: 2 3.004058 2.700000 Bayes
## 247: 2 3.010219 2.750000 Bayes
## 248: 2 3.016359 2.800000 Bayes
## 249: 2 3.022480 2.850000 Bayes
## 250: 2 3.028586 2.900000 BayesBelow, we consider only the grid points that do not overlap the text labels.
on.text <- function(V1, V2){
V2 <= max(error.text$V2.top) & V1 <= text.V1.prop
}
show.grid <- boundary.grid[!on.text(V1, V2),]
show.grid## validation.fold neighbors V1 V2 label set fold data.i
## <int> <num> <num> <num> <char> <char> <int> <int>
## 1: 0 7 0.1 -2.0 0 grid NA 10028
## 2: 0 7 0.2 -2.0 0 grid NA 10029
## 3: 0 7 0.3 -2.0 0 grid NA 10030
## 4: 0 7 0.4 -2.0 0 grid NA 10031
## 5: 0 7 0.5 -2.0 0 grid NA 10032
## ---
## 6395: 0 7 3.8 2.9 1 grid NA 16827
## 6396: 0 7 3.9 2.9 1 grid NA 16828
## 6397: 0 7 4.0 2.9 1 grid NA 16829
## 6398: 0 7 4.1 2.9 1 grid NA 16830
## 6399: 0 7 4.2 2.9 1 grid NA 16831
## probability pred.label is.error prediction
## <num> <char> <lgcl> <char>
## 1: 0.0000000 0 NA <NA>
## 2: 0.0000000 0 NA <NA>
## 3: 0.0000000 0 NA <NA>
## 4: 0.0000000 0 NA <NA>
## 5: 0.0000000 0 NA <NA>
## ---
## 6395: 0.5714286 1 NA <NA>
## 6396: 0.5714286 1 NA <NA>
## 6397: 0.5714286 1 NA <NA>
## 6398: 0.5714286 1 NA <NA>
## 6399: 0.5714286 1 NA <NA>The scatterplot below reproduces the 7-Nearest-Neighbors classifier of the original Figure.
label.colors <- c(
"0"="#377EB8",
"1"="#FF7F00")
scatterPlotStatic <- ggplot()+
theme_bw()+
theme(axis.text=element_blank(),
axis.ticks=element_blank(),
axis.title=element_blank())+
ggtitle("7-Nearest Neighbors")+
scale_color_manual(values=label.colors)+
scale_linetype_manual(values=classifier.linetypes)+
geom_point(aes(
V1, V2, color=label),
size=0.2,
data=show.grid)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
size=1,
data=pred.boundary)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
color=set.colors[["Bayes"]],
size=1,
data=Bayes.boundary)+
geom_point(aes(
V1, V2, color=label),
fill=NA,
size=3,
shape=21,
data=show.points)+
geom_text(aes(
text.V1.error, V2.bottom, label=paste(set, "Error:")),
data=error.text,
hjust=0)+
geom_text(aes(
text.V1.prop, V2.bottom, label=sprintf("%.3f", error.prop)),
data=error.text,
hjust=1)
scatterPlotStatic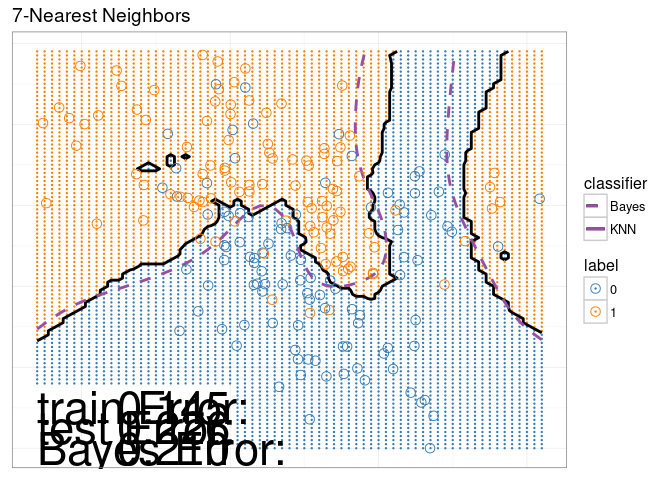
Combined plots
Finally, we combine the two ggplots and render them as an animint.
animint(errorPlotStatic, scatterPlotStatic)
This data viz does have three interactive legends, but it is static in the sense that it displays only the model predictions for 7-Nearest Neighbors.
Select the number of neighbors using interactivity
In this section we propose an interactive re-design which allows the user to select K, the number of neighbors in the K-Nearest-Neighbors classifier.
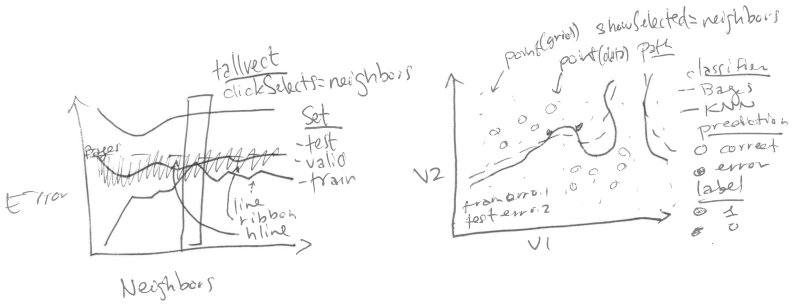
Clickable error curves plot
We begin with a re-design of the error curves plot.
Note the following changes: * add a selector for the number of neighbors (geom_tallrect). * change the Bayes decision boundary from geom_hline with a legend entry, to a geom_segment with a text label. * add a linetype legend to distinguish error rates from the Bayes and KNN models. * change the error bars (geom_linerange) to error bands (geom_ribbon).
The only new data that we need to define are the endpoints of the segment that we will use to plot the Bayes decision boundary. Note that we also re-define the set “test” to emphasize the fact that the Bayes error is the best achievable error rate for test data.
Bayes.segment <- data.table(
Bayes.error,
classifier="Bayes",
min.neighbors=1,
max.neighbors=29)
Bayes.segment$set <- "test"We also add an error variable to the data tables that contain the prediction error of the K-Nearest-Neighbors models. This error variable will be used for the linetype legend.
validation.error$classifier <- "KNN"
other.error$classifier <- "KNN"We re-define the plot of the error curves below. Note that * We use showSelected in geom_text and geom_ribbon, so that they will be hidden when the interactive legends are clicked. * We use clickSelects in geom_tallrect, to select the number of neighbors. Clickable geoms should be last (top layer) so that they are not obscured by non-clickable geoms (bottom layers).
set.colors <- c(
test="#984EA3",#purple
validation="#4DAF4A",#green
Bayes="#984EA3",#purple
train="black")
errorPlot <- ggplot()+
ggtitle("Select number of neighbors")+
theme_bw()+
theme_animint(height=500)+
geom_text(aes(
min.neighbors, error.prop,
color=set, label="Bayes"),
showSelected="classifier",
hjust=1,
data=Bayes.segment)+
geom_segment(aes(
min.neighbors, error.prop,
xend=max.neighbors, yend=error.prop,
color=set,
linetype=classifier),
showSelected="classifier",
data=Bayes.segment)+
scale_color_manual(values=set.colors, breaks=names(set.colors))+
scale_fill_manual(values=set.colors)+
guides(fill="none", linetype="none")+
scale_linetype_manual(values=classifier.linetypes)+
ylab("Misclassification Errors")+
scale_x_continuous(
"Number of Neighbors",
limits=c(-1, 30),
breaks=c(1, 10, 20, 29))+
geom_ribbon(aes(
neighbors, ymin=mean-sd, ymax=mean+sd,
fill=set),
showSelected=c("classifier", "set"),
alpha=0.5,
color="transparent",
data=validation.error)+
geom_line(aes(
neighbors, mean, color=set,
linetype=classifier),
showSelected="classifier",
data=validation.error)+
geom_line(aes(
neighbors, error.prop, group=set, color=set,
linetype=classifier),
showSelected="classifier",
data=other.error)+
geom_tallrect(aes(
xmin=neighbors-1, xmax=neighbors+1),
clickSelects="neighbors",
alpha=0.5,
data=validation.error)
errorPlot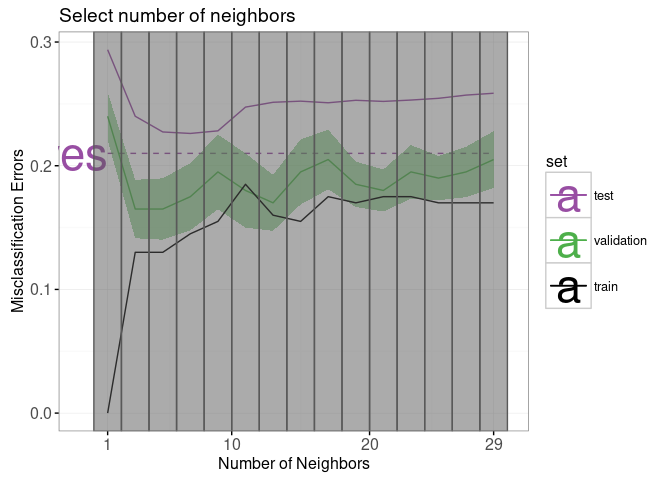
Feature space plot that shows the selected number of neighbors
Next, we focus on a re-design of the feature space plot. In the previous section we considered only the subset of data from the model with 7 neighbors. Our re-design includes the following changes: * We use neighbors as a showSelected variable. * We add a legend to show which training data points are mis-classified. * We use equal spaced coordinates so that visual distance (pixels) is the same as the Euclidean distance in the feature space.
show.data <- data.all.folds[validation.fold==0,]
show.points <- show.data[set=="train",]
show.points## validation.fold neighbors V1 V2 label set fold
## <int> <num> <num> <num> <fctr> <char> <int>
## 1: 0 1 2.526092968 0.3210504 0 train 5
## 2: 0 1 0.366954472 0.0314621 0 train 8
## 3: 0 1 0.768219076 0.7174862 0 train 6
## 4: 0 1 0.693435680 0.7771940 0 train 10
## 5: 0 1 -0.019836616 0.8672537 0 train 6
## ---
## 2996: 0 29 0.256750222 2.2936046 1 train 1
## 2997: 0 29 1.925173384 0.1650526 1 train 3
## 2998: 0 29 1.301941035 0.9921996 1 train 6
## 2999: 0 29 0.008130556 2.2422639 1 train 4
## 3000: 0 29 -0.196246334 0.5514036 1 train 8
## data.i probability pred.label is.error prediction
## <int> <num> <char> <lgcl> <char>
## 1: 16832 0.0000000 0 FALSE correct
## 2: 16833 0.0000000 0 FALSE correct
## 3: 16834 0.0000000 0 FALSE correct
## 4: 16835 0.0000000 0 FALSE correct
## 5: 16836 0.0000000 0 FALSE correct
## ---
## 2996: 17027 0.8275862 1 FALSE correct
## 2997: 17028 0.5517241 1 FALSE correct
## 2998: 17029 0.7931034 1 FALSE correct
## 2999: 17030 0.7586207 1 FALSE correct
## 3000: 17031 0.3793103 0 TRUE errorBelow, we compute the predicted decision boundaries separately for each K-Nearest-Neighbors model.
boundary.grid <- show.data[set=="grid",]
boundary.grid[, label := pred.label]
show.grid <- boundary.grid[!on.text(V1, V2),]
pred.boundary <- boundary.grid[, getBoundaryDF(probability), by=neighbors]
pred.boundary$classifier <- "KNN"
pred.boundary## neighbors path.i V1 V2 classifier
## <num> <int> <num> <num> <char>
## 1: 1 1 -2.600000 -1.025000 KNN
## 2: 1 1 -2.550000 -1.000000 KNN
## 3: 1 1 -2.500000 -0.975000 KNN
## 4: 1 1 -2.450000 -0.950000 KNN
## 5: 1 1 -2.450000 -0.900000 KNN
## ---
## 4488: 29 2 2.800000 1.897619 KNN
## 4489: 29 2 2.795238 1.900000 KNN
## 4490: 29 2 2.800000 1.902381 KNN
## 4491: 29 2 2.800990 1.900000 KNN
## 4492: 29 2 2.800000 1.897619 KNNInstead of showing the number of neighbors in the plot title, below we create a geom_text element that will be updated based on the number of selected neighbors.
show.text <- show.grid[, list(
V1=mean(range(V1)), V2=3.05), by=neighbors]Below we compute the position of the text in the bottom left, which we will use to display the error rate of the selected model.
other.error[, V2.bottom := rep(
text.V2.bottom + text.height * 1:2, l=.N)]Below we re-define the Bayes error data without a neighbors column, so that it appears in each showSelected subset.
Bayes.error <- data.table(
set="Bayes",
error.prop=0.21)Finally, we re-define the ggplot, using neighbors as a showSelected variable in the point, path, and text geoms.
scatterPlot <- ggplot()+
ggtitle("Mis-classification errors in train set")+
theme_bw()+
theme_animint(width=500, height=500)+
xlab("Input feature 1")+
ylab("Input feature 2")+
coord_equal()+
scale_color_manual(values=label.colors)+
scale_linetype_manual(values=classifier.linetypes)+
geom_point(aes(
V1, V2, color=label),
showSelected="neighbors",
size=0.2,
data=show.grid)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
showSelected="neighbors",
size=1,
data=pred.boundary)+
geom_path(aes(
V1, V2, group=path.i, linetype=classifier),
color=set.colors[["test"]],
size=1,
data=Bayes.boundary)+
geom_point(aes(
V1, V2, color=label,
fill=prediction),
showSelected="neighbors",
size=3,
shape=21,
data=show.points)+
scale_fill_manual(values=c(error="black", correct="transparent"))+
geom_text(aes(
text.V1.error, text.V2.bottom, label=paste(set, "Error:")),
data=Bayes.error,
hjust=0)+
geom_text(aes(
text.V1.prop, text.V2.bottom, label=sprintf("%.3f", error.prop)),
data=Bayes.error,
hjust=1)+
geom_text(aes(
text.V1.error, V2.bottom, label=paste(set, "Error:")),
showSelected="neighbors",
data=other.error,
hjust=0)+
geom_text(aes(
text.V1.prop, V2.bottom, label=sprintf("%.3f", error.prop)),
showSelected="neighbors",
data=other.error,
hjust=1)+
geom_text(aes(
V1, V2,
label=paste0(
neighbors,
" nearest neighbor",
ifelse(neighbors==1, "", "s"),
" classifier")),
showSelected="neighbors",
data=show.text)Before compiling the interactive data viz, we print a static ggplot with a facet for each value of neighbors.
scatterPlot+
facet_wrap("neighbors")+
theme(panel.margin=grid::unit(0, "lines"))
Combined interactive data viz
Finally, we combine the two plots in a single data viz with neighbors as a selector variable.
animint(
errorPlot,
scatterPlot,
first=list(neighbors=7),
time=list(variable="neighbors", ms=3000))
Note that neighbors is used as a time variable, so animation shows the predictions of the different models.
Select the number of cross-validation folds using interactivity
In this section we discuss a second re-design which allows the user to select the number of folds used to compute the validation error curve.
The for loop below computes the validation error curve for several different values of n.folds.
error.by.folds <- list()
error.by.folds[["10"]] <- data.table(n.folds=10, validation.error)
for(n.folds in c(3, 5, 15)){
set.seed(2)
mixture <- with(ESL.mixture, data.table(x, label=factor(y)))
mixture$fold <- sample(rep(1:n.folds, l=nrow(mixture)))
only.validation.list <- future.apply::future_lapply(
1:n.folds, function(validation.fold){
one.fold <- OneFold(validation.fold)
data.table(validation.fold, one.fold[set=="validation"])
})
only.validation <- do.call(rbind, only.validation.list)
only.validation.error <- only.validation[, list(
error.prop=mean(is.error)
), by=.(set, validation.fold, neighbors)]
only.validation.stats <- only.validation.error[, list(
mean=mean(error.prop),
sd=sd(error.prop)/sqrt(.N)
), by=.(set, neighbors)]
error.by.folds[[paste(n.folds)]] <-
data.table(n.folds, only.validation.stats, classifier="KNN")
}## Warning: UNRELIABLE VALUE: One of the 'future.apply' iterations
## ('future_lapply-1') unexpectedly generated random numbers without declaring so.
## There is a risk that those random numbers are not statistically sound and the
## overall results might be invalid. To fix this, specify 'future.seed=TRUE'. This
## ensures that proper, parallel-safe random numbers are produced via the
## L'Ecuyer-CMRG method. To disable this check, use 'future.seed = NULL', or set
## option 'future.rng.onMisuse' to "ignore".## Warning: UNRELIABLE VALUE: One of the 'future.apply' iterations
## ('future_lapply-2') unexpectedly generated random numbers without declaring so.
## There is a risk that those random numbers are not statistically sound and the
## overall results might be invalid. To fix this, specify 'future.seed=TRUE'. This
## ensures that proper, parallel-safe random numbers are produced via the
## L'Ecuyer-CMRG method. To disable this check, use 'future.seed = NULL', or set
## option 'future.rng.onMisuse' to "ignore".## Warning: UNRELIABLE VALUE: One of the 'future.apply' iterations
## ('future_lapply-1') unexpectedly generated random numbers without declaring so.
## There is a risk that those random numbers are not statistically sound and the
## overall results might be invalid. To fix this, specify 'future.seed=TRUE'. This
## ensures that proper, parallel-safe random numbers are produced via the
## L'Ecuyer-CMRG method. To disable this check, use 'future.seed = NULL', or set
## option 'future.rng.onMisuse' to "ignore".## Warning: UNRELIABLE VALUE: One of the 'future.apply' iterations
## ('future_lapply-2') unexpectedly generated random numbers without declaring so.
## There is a risk that those random numbers are not statistically sound and the
## overall results might be invalid. To fix this, specify 'future.seed=TRUE'. This
## ensures that proper, parallel-safe random numbers are produced via the
## L'Ecuyer-CMRG method. To disable this check, use 'future.seed = NULL', or set
## option 'future.rng.onMisuse' to "ignore".## Warning: UNRELIABLE VALUE: One of the 'future.apply' iterations
## ('future_lapply-1') unexpectedly generated random numbers without declaring so.
## There is a risk that those random numbers are not statistically sound and the
## overall results might be invalid. To fix this, specify 'future.seed=TRUE'. This
## ensures that proper, parallel-safe random numbers are produced via the
## L'Ecuyer-CMRG method. To disable this check, use 'future.seed = NULL', or set
## option 'future.rng.onMisuse' to "ignore".## Warning: UNRELIABLE VALUE: One of the 'future.apply' iterations
## ('future_lapply-2') unexpectedly generated random numbers without declaring so.
## There is a risk that those random numbers are not statistically sound and the
## overall results might be invalid. To fix this, specify 'future.seed=TRUE'. This
## ensures that proper, parallel-safe random numbers are produced via the
## L'Ecuyer-CMRG method. To disable this check, use 'future.seed = NULL', or set
## option 'future.rng.onMisuse' to "ignore".validation.error.several <- do.call(rbind, error.by.folds)The code below computes the minimum of the error curve for each value of n.folds.
min.validation <- validation.error.several[, .SD[which.min(mean),], by=n.folds]The code below creates a new error curve plot with two facets.
facets <- function(df, facet){
data.frame(df, facet=factor(facet, c("n.folds", "Misclassification Errors")))
}
errorPlotNew <- ggplot()+
ggtitle("Select number of folds and neighbors")+
theme_bw()+
theme_animint(height=500)+
theme(panel.margin=grid::unit(0, "cm"))+
facet_grid(facet ~ ., scales="free")+
geom_text(aes(
min.neighbors, error.prop,
color=set, label="Bayes"),
showSelected="classifier",
hjust=1,
data=facets(Bayes.segment, "Misclassification Errors"))+
geom_segment(aes(
min.neighbors, error.prop,
xend=max.neighbors, yend=error.prop,
color=set,
linetype=classifier),
showSelected="classifier",
data=facets(Bayes.segment, "Misclassification Errors"))+
scale_color_manual(values=set.colors, breaks=names(set.colors))+
scale_fill_manual(values=set.colors, breaks=names(set.colors))+
guides(fill="none", linetype="none")+
scale_linetype_manual(values=classifier.linetypes)+
ylab("")+
scale_x_continuous(
"Number of Neighbors",
limits=c(-1, 30),
breaks=c(1, 10, 20, 29))+
geom_ribbon(aes(
neighbors, ymin=mean-sd, ymax=mean+sd,
fill=set),
showSelected=c("classifier", "set", "n.folds"),
alpha=0.5,
color="transparent",
data=facets(validation.error.several, "Misclassification Errors"))+
geom_line(aes(
neighbors, mean, color=set,
linetype=classifier),
showSelected=c("classifier", "n.folds"),
data=facets(validation.error.several, "Misclassification Errors"))+
geom_line(aes(
neighbors, error.prop, group=set, color=set,
linetype=classifier),
showSelected="classifier",
data=facets(other.error, "Misclassification Errors"))+
geom_tallrect(aes(
xmin=neighbors-1, xmax=neighbors+1),
clickSelects="neighbors",
alpha=0.5,
data=validation.error)+
geom_point(aes(
neighbors, n.folds, color=set),
clickSelects="n.folds",
size=9,
data=facets(min.validation, "n.folds"))The code below previews the new error curve plot, adding an additional facet for the showSelected variable.
errorPlotNew+facet_grid(facet ~ n.folds, scales="free")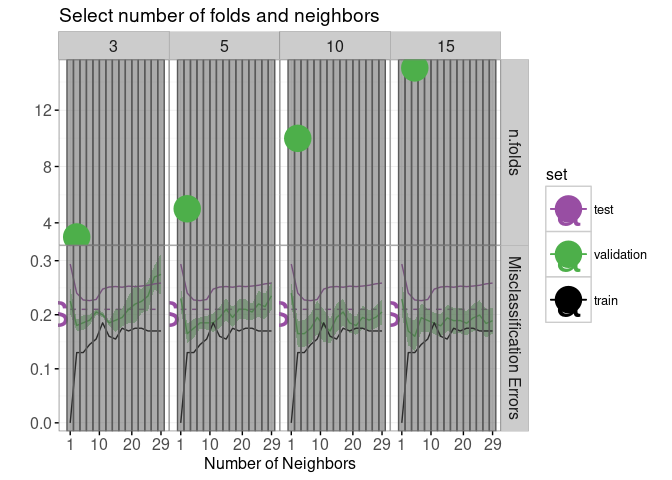
The code below creates an interactive data viz using the new error curve plot.
animint(
errorPlotNew,
scatterPlot,
first=list(neighbors=7, n.folds=10))
Chapter summary and exercises
We showed how to add two interactive features to a data visualization of predictions of the K-Nearest-Neighbors model. We started with a static data visualization which only showed predictions of the 7-Nearest-Neighbors model. Then, we created an interactive re-design which allowed selecting K, the number of neighbors. We did another re-design which added a facet for selecting the number of cross-validation folds.
Exercises:
- Make it so that text error rates in the bottom left of the second plot are hidden after clicking the legend entries for Bayes, train, test. Hint: you can either use one
geom_textwithshowSelected=c(selectorNameColumn="selectorValueColumn")(as explained in Chapter 14) or twogeom_text, each with a different showSelected parameter. - The probability column of the show.grid data table is the predicted probability of class 1. How would you re-design the visualization to show the predicted probability rather than the predicted class at each grid point? The main challenge is that probability is a numeric variable, but ggplot2 enforces that each scale must be either continuous or discrete (not both). You could use a continuous fill scale, but then you would have to use a different scale to show the prediction variable.
- Add a new plot that shows the relative sizes of the train, validation, and test sets. Make sure that the plotted size of the validation and train sets change based on the selected value of
n.folds. - So far, the feature space plots only showed model predictions and errors for the entire train data set (validation.fold==0). Create a re-design which includes a new plot or facet for selecting validation.fold, and a facetted feature space plot (one facet for train set, one facet for validation set).
Next, Chapter 11 explains how to visualize the Lasso, a machine learning model.
